Las Fracciones: Tutorial Ùtil para el Aula

 

El concepto matemático de fracción corresponde a la idea intuitiva de dividir una totalidad en partes iguales, como cuando hablamos, por ejemplo, de un cuarto de hora, de la mitad de un pastel, o de las dos terceras partes de un depósito de gasolina.  Tres cuartos de hora no son, evidentemente, la misma cosa que las tres cuartas partes de un pastel, pero se “calculan” de la misma manera: dividiendo la totalidad (una hora, o el pastel) en cuatro partes iguales y tomando luego tres de esas partes.  Por esta razón, en ambos casos, se habla de dividir dicha unidad (una hora, un pastel, etc.) en 4 partes iguales y tomar luego 3 de dichas partes.
Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.

La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.

TÉRMINOS DE UNA FRACCIÓN

a	Numerador
—	-
b	Denominador

El Numerador indica el número de partes iguales  que se han tomado o considerado de un entero. El  Denominador indica el número de partes iguales en que se ha dividido un entero.

Por ejemplo, la fracción   3 / 4  (se lee tres cuartos) tiene como numerador al 3 y como denominador al 4. El 3 significa que se han considerado 3 partes de un total de 4 partes en que se dividió el entero o el todo.

La fracción  1 / 7 (se lee un séptimo) tiene como numerador al 1 y como denominador al 7. El numerador indica que se ha considerado 1 parte de un total de 7 (el denominador indica que el entero se dividió en 7 partes iguales).

Ejemplos:

Hay 8 partes de las cuales se han pintado 5, por lo tanto, la fracción que representa matemáticamente este dibujo es 5 / 8 (se lee cinco octavos).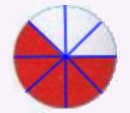

Hay 3 partes pintadas de un total de 5. Esto se representa como 3 / 5 (se lee tres quintos)

Debes tener presente que existen distintas posibilidades para representar gráficamente una fracción, es decir, se puede representar con distintos dibujos; lo importante es tener siempre presente el  concepto de fracción.

 Por ejemplo, la fracción 5 / 8, que ya vimos arriba, está representada a continuación de otras dos formas distintas:

Hay 5 partes pintadas de un total de 8 partes. Esto se representa como 5 / 8 (se lee cinco octavos)

Hay 5 partes pintadas de un total de 8 partes. Esto se representa como 5 / 8 (se lee cinco octavos)

Otros ejemplos:

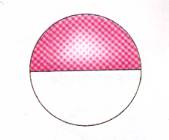
Hay 1 parte pintada de un total de 2 partes. Esto se representa como 1 / 2 (se lee un medio)

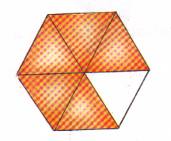
Hay 5 partes pintadas de un total de 6 partes. Esto se representa como 5 / 6 (se lee cinco sextos)